
문제
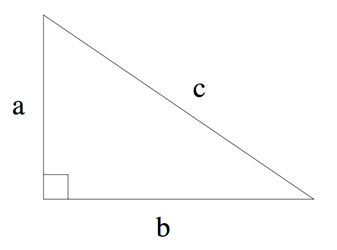
컴퓨터를 이용하면 수학 계산이 조금 쉬워진다. 다음과 같은 예를 살펴보자. 세 변의 길이가 a, b, c(c는 빗변)이면서 a2+b2=c2를 만족하는 삼각형을 직각삼각형이라고 한다. 이 공식은 피타고라스의 법칙이라고 한다.
직각 삼각형의 두 변의 길이가 주어졌을 때, 한 변의 길이를 구하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직각 삼각형의 세 변의 길이 a, b, c가 주어진다. a, b, c중 하나는 -1이며, -1은 알 수 없는 변의 길이이다. 다른 두 수는 10,000보다 작거나 같은 자연수이다.
입력의 마지막 줄에는 0이 세 개 주어진다.
출력
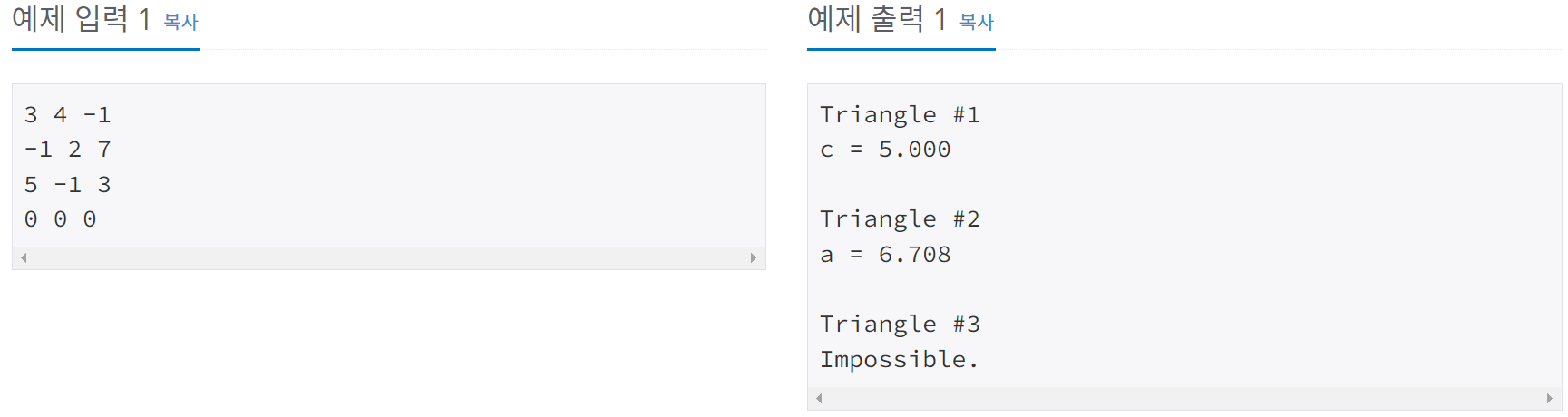
각 테스트 케이스에 대해서, 입력으로 주어진 길이로 직각 삼각형을 만들 수 있다면, "s = l"을 출력한다. s는 길이가 주어지지 않은 변의 이름이고, l은 길이이다. l은 소수점 셋째 자리까지 출력한다. 삼각형을 만들 수 없는 경우에는 "Impossible."을 출력한다.
출처
ICPC > Regionals > Europe > Southwestern European Regional Contest > SWERC 1997 PB번

일단 틀렸습니다. 의 결과를 받은 코드를 먼저 공개합니다.
#include<cstdio>
#include<cmath>
int main(){
float a,b,c;
int ct = 1;
while(scanf("%f %f %f",&a,&b,&c)){
if(a == 0 && b == 0 && c == 0) break;
float res = 0.000;
if(a == -1){
res = sqrt(c*c-b*b);
}else if(b == -1){
res = sqrt(c*c-a*a);
}else{
res = sqrt(a*a+b*b);
}
printf("Triangle #%d\n",ct++);
if(a >= c || b >= c){
printf("Impossible.\n\n");
}else{
if(a == -1) printf("a");
else if(b == -1) printf("b");
else printf("c");
printf(" = %.3f\n\n",res);
}
}
}음.. 왜 틀렸을지 잘 모르겠네요.
다음은 정답 코드를 공개합니다.
#include<cstdio>
#include<cmath>
int main(){
float a,b,c;
int ct = 1;
while(scanf("%f %f %f",&a,&b,&c)){
if(a == 0 && b == 0 && c == 0) break;
float res = 0.000;
if(a == -1){
res = sqrt(c*c-b*b);
}else if(b == -1){
res = sqrt(c*c-a*a);
}else{
res = sqrt(a*a+b*b);
}
printf("Triangle #%d\n",ct++);
if(c != -1 && (a >= c || b >= c)){
printf("Impossible.\n\n");
}else{
if(a == -1) printf("a");
else if(b == -1) printf("b");
else printf("c");
printf(" = %.3f\n\n",res);
}
}
}아하. 조건을 하나 빼먹었네요. c 역시 -1 이 되었을 때 이를 검출하는 조건이 없어, 이전 코드에서 정답 판정을 받지 못 했던 것 같습니다. 조건이 까다롭고 많은 것은 실수든 아니든 놓치기가 쉽죠. 이런 문제일 수록 손으로 먼저 모든 조건을 나열한 다음에 조건문 작성을 시작해야 합니다. 또한, if else 로 구분한다고 할지라도 else if 를 최대한 많이 직접적으로 써보는 것이 오답률을 줄일 수 있는 방법입니다. 이 문제에는 안 어울리지만 이런 식으로도 작성할 수 있겠죠.
if(a == -1){
res = sqrt(c*c-b*b);
}else if(b == -1){
res = sqrt(c*c-a*a);
}else if(c == -1){
res = sqrt(a*a+b*b);
}else {
res = sqrt(a*a+b*b);
}이 경우 아래 두 조건은 동일하지만, 다른 문제의 경우에는 보다 직관적으로 조건 문이 확인할 수 있기 때문에 오답률을 줄일 수가 있습니다.
이상입니다.



